透视投影
对透视投影的深入思考
投影变换是整个渲染管线里,设计得最复杂的,也最巧妙的一次变换。
前因
在GAMES101中,我只是大概了解了透视投影矩阵所做出的变换,将视椎体中的点全部映射到近平面上,再将近平面缩放成规则观察体(CVV空间)。
而在tinyrenderer中,我见到了不一样的透视投影矩阵。
关于透视投影的插值矫正,tinyrenderer直接忽略了这点,GAMES101中也没有做更详细的讲解,以至于我在看到透视除法等一系列操作时摸不到头脑。
于是,我去开始查找资料,为什么要做透视投影的插值矫正?但网上得到的答案大多都很简短、类似。类似于:重心坐标插值要在线性空间中插值,世界空间、观察空间中的坐标都是线性的,而经过透视投影变换后,是非线性的。于是以屏幕坐标插值出的结果是畸形的,当线性坐标下(例如观察坐标)的插值结果才是正确的。
这番解释虽然大概说明了要做透视插值矫正的必要性,但距离实际应用还是一头雾水。我到底该怎么从屏幕坐标这个非线性空间,插值得到线性空间坐标?透视投影变换的步骤究竟是什么?透视除法除以的w分量又究竟是什么,为什么要这么做?
于是,我展开了深入的理解。
理解前的统一定义
首先,为了统一坐标系、矩阵等问题,我会从以下方式思考:
- 向量默认为列向量
- 矩阵默认为列主序
- 变换默认为矩阵左乘
- 坐标系默认为右手系
- 摄像机默认处于原点,lookat方向-z,向上方向+y
投影变换的目的
坐标转换到观察空间后,由于直接使用摄像机的平截头体进行裁剪比较复杂(平截头体的边界方程求交困难),所以需要将其转化到裁剪空间(Clip空间 )。
从观察空间到裁剪空间的变换叫做投影变换。Project
裁剪空间变换的思路是,对视椎体进行缩放,使远裁剪面缩放至近裁剪面大小,然后将这个长方体缩放至标准立方体移动到原点,使坐标的w分量表示裁剪范围,此时,只需要简单的比较x,y,z和w分量的大小即可裁剪图元。
虽然叫做投影变换,但是投影变换并没有进行真正的投影。
这一篇主要讲透视投影
透视投影变换步骤
- 从视椎体内一点投影到近裁剪面
- 由近裁剪面缩放至规则观察体(CVV空间),得到clip坐标(此时clip坐标还没有除以w变成3D坐标,仍是齐次坐标)
对相机空间中的顶点,如果在视锥体中,则变换后就在CVV中。如果在视锥体外,变换后就在CVV外。CVV本身的规则性对于多边形的裁剪很有利。
透视投影简易模型理解
首先,我们明确我们的需求:将观察空间中视椎体中的坐标点 (x, y, z, 1),通过透视投影,转化到近平面上的点 (x’, y’, z’, 1) 中去。
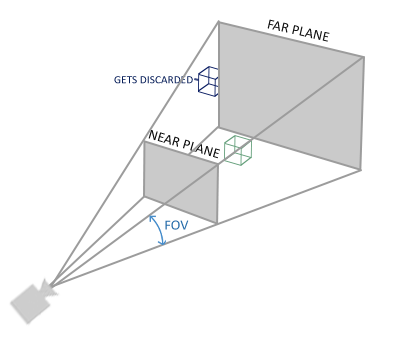
那么我们可以很简单的得到 z’ = Near,那么由于近平面值Near是固定的,先不妨假设为1,则
由相似三角形可得:
- z’ = 1 (z’ = Near)
- x’ = x/z (x’ = x * Near / z)
- y’ = y/z (y’ = y * Near / z)
- w = 1
那么就可以推出tinyrenderer中的透视矩阵:
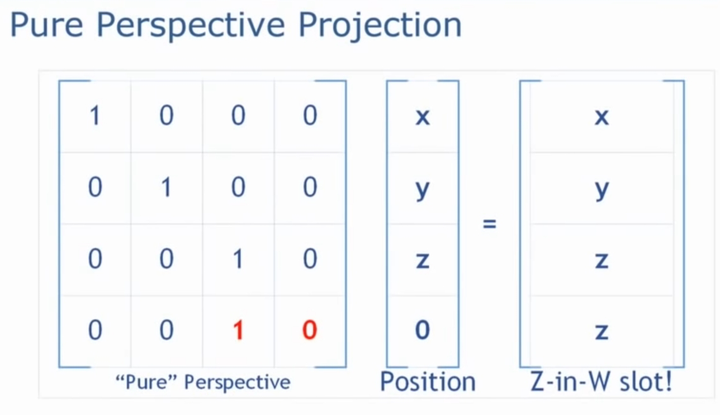
因采用右手系,这里红色的1应该是-1
注意到M的最后一行不是(0 0 0 1)而是(0 0 -1 0),因此可以看出透视变换不是一种仿射变换,它是非线性的。
经过这个矩阵变换,就可以得到(x’ = x, y’ = y, z’ = z, w’ = z),经过齐次除法,xy映射到x’ = x/z,y’ = y/z,z’ = 1。这正是我们想要的变换。
我们将透视投影变换的系数储存在了w分量里,只要进行透视除法,就是非线性的(x’, y’, z’)坐标,而不考虑w分量,(x, y, z)仍是线性可插值的。
数学推导
推荐看这篇文章:图形学基础之透视校正插值
经过推导,我们发现:
当我们从视角空间到透视投影到屏幕空间后,我们的线性变换并不是x, y, z的线性变换,而是x, y, 1/z的线性变换。因此在屏幕空间上的插值需要做透视校正,否则会出现不正确的情况。
为什么是1/z的线性变换呢,在透视投影中,我们的视椎体是一个不规则立方体,将点(x, y, z)中的x, y映射到屏幕(近平面)上时会根据其z的值进行压缩,其公式是:
- x’ = Near/z * x
- y’ = Near/z * y
可以发现x’, y’和x, y的关系是1/z的关系。
在齐次坐标中 ,因此我们将z保存在w的位置,将x, y, z在透视投影下的线性变换都乘以z。这样
就是关于x, y, z的线性变换。
因此所谓的透视除法,就是在透视投影后还原x, y, z真实的屏幕空间值的过程。
真实模型理解
下面来看看网上最常见的透视矩阵书写形式:
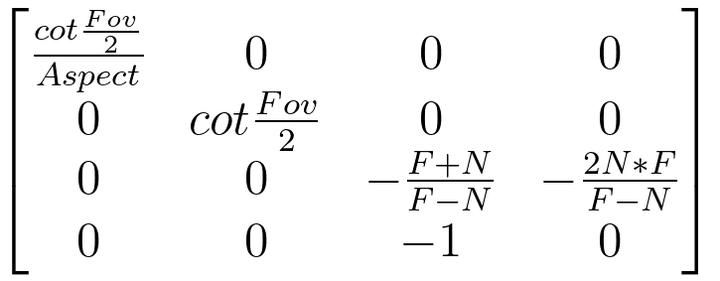
其实这么写反而妨碍了我们的直观理解,由Aspect、Fov与w(width)、h(height)、N(Near)、F(Far)的关系,我们应当写成如下形式:
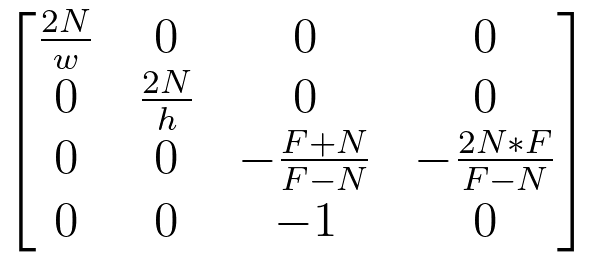
发现了吗,和透视矩阵之母Pure Perspective Projection的区别,第一列第一行的1变为了N*(2/w)这么一个缩放值。
2/w很好理解,是将近平面的宽缩放到长度2;
乘上N ,是因为考虑到齐次除法xyz分量要除以w分量,矩阵转化后的w分量等于转化前的z分量相反数。
故x’/w’= x/z, y’/w’ = y/z,是我们要的投影到近平面为1的值,这个值乘上N就相当于映射到了近平面,即true x’ =(N/z)*(2/w)。 相应的,mat11的值1变化为2N/h。
总结
关于透视投影的矫正,通过将原始的z值存储在w分量中。
透视校正插值使用线性的深度值和非线性空间下的插值系数s来计算出线性空间下的插值系数t,并用t来对顶点属性进行插值。
最后得到的(x’, y’, z’, w)中,x‘、y’已经是xy乘过Near了,再除以z不就是屏幕空间吗。
- x’ = x * Near / z
- y’ = y * Near / z
- z = Near
- w = 1
